Altitudes and Orthocenters

By

Cassian Mosha

 

 

Given triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully. Prove:

 

                                                  

 

                                                

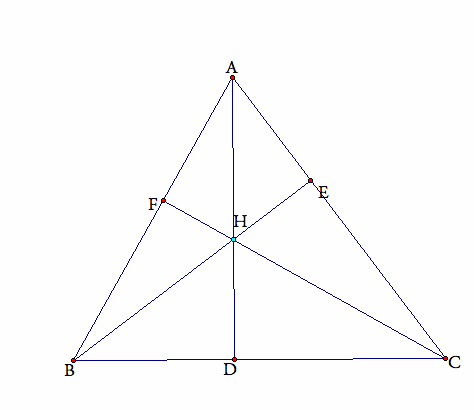
Figure 1

 

   What if ABC is an obtuse triangle?

 

Proof:

Let's denote area of triangle ABC as T. Then 2T= |BC||AD| =|AB||CF| =|AC||BE|

Also T is the sum of the areas of triangles AHB, AHC and BHC

So |AB||FH|+|AC||EH|+|BC||DH| =2T

Dividing both sides of the latter equation by 2T, and substituting, we get

||AB||FH|/|AB}}CF| + |AC||EH|/|AC||BE| +|BC||DH|/|BC||AD|| =1

Reducing the fractions we get |FH|/|CF|+|EH|/|BE|+|DH|/|AD|=1 something that we wanted.

Now to get the second result it follows that by subtracting the last result above equation from ||CF|/|CF|+|BE|/|BE|+|AD|/|AD|=3, we will get the second required result.QED

If triangle ABC is an obtuse triangle the result above will not hold anymore since point H the orthocener will be lying outside triangle ABC as shown in the sketch below. To make our result above hold we will refer to triangle HBC.

 

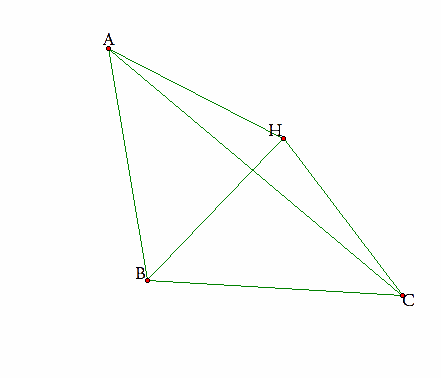
Figure 2

 

Return